| Часть 1: вопросы 1-50 |
| 1. | Укажите верное утверждение: а) если в ограничениях одной из сопряженных задач встречается равенство, то в другой есть переменная, не ограниченная в знаке; б) если решение прямой задачи на минимум обращает i-е ограничение в строгое равенство, то соответствуящая двойственная переменная отлична от нуля; в) если прямая задача на минимум, то ее допустимое решение не больше допустимого решения сопряженной задачи. узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 2. | Укажите верное утверждение: а) если прямая задача на максимум не ограничена сверху, то двойственная не имеет решения; б) если прямая задачи на максимум не имеет решения, то двойственная задача не ограничена; в) если прямая задача на минимум, то ее допустимое решение не больше допустимого решения сопряженной задачи. узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 3. | Укажите верное утверждение: а) если прямая задача на минимум, то ее допустимое решение не больше допустимого решения сопряженной задачи; б) если прямая задача на минимум, то ее допустимое решение не меньше допус- тимого решения сопряженной задачи; в) если прямая задача на максимум не имеет решения, то двойственная задача не ограничена. узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 4. | Укажите неверное утверждение: а) если в ограничениях одной из сопряженных задач встречается равенство, то в другой есть переменная, не ограниченная в знаке; б) если прямая задача на максимум не ограничена сверху, то двойственная не имеет решения; в) если прямая задача на минимум, то ее допустимое решение не больше допустимого решения сопряженной. узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 5. | Укажите неверное утверждение: а) если в ограничениях одной из сопряженных задач встречается равенство, то в другой есть переменная, не ограниченная в знаке; б) если прямая задача на максимум не ограничена сверху, то двойственная не имеет решения; в) равенство значений целевых функций прямой и двойственной задачи является единственным условием, необходимым для доказательства оптимальности выбранных значений переменных обеих задач. узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 6. | Укажите неверное утверждение: а) если в ограничениях одной из сопряженных задач встречается равенство, то в другой есть переменная, не ограниченная в знаке; б) если решение двойственной задачи на максимум обращает i-ое ограничение в строгое неравенство, то соответствующая переменная прямой задачи больше нуля; в) если в сопряженых задачах имеются допустимые решения, при которых целевые функции совпадают, то решения оптимальны. узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 7. | Укажите неверное утверждение: а) если двойственная задача на минимум, то ее допустимое решение не больше допустимого решения сопряженной задачи; б) в любой паре допустимых решений прямой и двойственной задач, значение целевой функции прямой задачи не может превышать значения целевой функции двойственной задачи, независимо от направления оптимизации; в) если прямая задача на минимум, то ее допустимое решение не меньше допустимого решения сопряженной задачи. узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 8. | Укажите неверное утверждение: а) если двойственная задача на минимум, то ее допустимое решение не больше допустимого решения сопряженной задачи; б) если обе сопряженные задачи имеют хотя бы по одному допустимому решению, то они имеют и оптимальное решение; в) если прямая задача на минимум не ограничена снизу, то двойственная не имеет решения. узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 9. | Укажите неверное утверждение: а) если обе сопряженные задачи имеют хотя бы по одному допустимому решению, то они имеют и оптимальное решение; б) если в сопряженных задачах имеются допустимуе решения, при которых целевые функции совпадают, то решение оптимальное; в) если прямая задача на максимум, то ее допустимое решение не больше допустимого решения сопряженной. узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 10. | Укажите неверное утверждение: а) если обе сопряженные задачи имеют хотя бы по одному допустимому решению, то они имеют и оптимальное решение; б) если в сопряженных задачах имеются допустимые решения, при которых целевые функции совпадают, то решения оптимальны; в) в любой паре допустимых решений прямой и двойственной задач, значение целевой функции прямой задачи не может превышать значения целевой функции двой- ственной задачи, независимо от направления оптимизации. узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 11. | Укажите неверное утверждение: а) если обе сопряженные задачи имеют хотя бы по одному допустимому решению, то они имеют и оптимальное решение; б) если решение двойственной задачи на максимум обращает i-ое ограничение в строгое неравенство, то соответствующая переменная прямой задачи больше нуля; в) если в ограничениях одной из сопряженных задач встречается равенство, то в другой есть переменная, не ограниченная в знаке. узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 12. | Укажите неверное утверждение: а) если обе сопряженные задачи имеют хотя бы по одному допустимому решению, то они имеют и оптимальное решение; б) при всяком изменении правой части ограничений прямой задачи изменяется и оптимальное решение двойственной задачи; в) если в сопряженных задачах имеются допустимые решения, при которых целевые функции совпадают, то решения оптимальны. узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 13. | Укажите неверное утверждение: а) если прямая задача на максимум не имеет решения, то двойственная не ограничена; б) если прямая задача на максимум не ограничена сверху, то двойственная не имеет решения; в) если прямая задача на минимум не ограничена снизу, то двойственная не имеет решения. узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 14. | Укажите неверное утверждение: а) если прямая задача на максимум не ограничена сверху, то двойственная не имеет решения; б) если решение прямой задачи на максимум обращает i-е ограничение в строгое неравенство, то соответствуящая двойственная переменная равна нулю; в) если прямая задача на минимум, то ее допустимое решение не меньше допустимого решения сопряженной задачи. узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 15. | Укажите неверное утверждение: а) если прямая задача на максимум не ограничена сверху, то двойственная задача не имеет решения; б) если двойственная задачи на минимум, то ее допустимое решение не больше допустимого решения сопряженной задачи; в) если в сопряженых задачах имеются допустимые решения, при которых целевые функции совпадают, то решения оптимальны. узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 16. | Укажите неверное утверждение: а) если прямая задача на максимум, то ее допустимое решение не больше допустимого решения сопряженной задачи; б) если прямая задача на максимум не ограничена сверху, то двойственная не имеет решения; в) если решение прямой задачи на максимум обращает i-ое ограничение в строгое равенство, то соответствующая двойственная переменная равна нулю. узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 17. | Укажите неверное утверждение: а) если прямая задача на максимум, то ее допустимое решение не больше допустимого решения сопряженной задачи; б) если обе сопряженные задачи имеют хотя бы по одному допустимому решению, то они имеют и оптимальное решение; в) при всяком измененении правой части ограничений прямой задачи, изменяется и оптимальное решение двойственной задачи. узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 18. | Укажите неверное утверждение: а) если прямая задача на максимум, то ее допустимое решение не больше допустимого решения сопряженной задачи; б) если прямая задача на минимум не ограничена снизу, то двойственная задача не имеет решения; в) при всяком измененении правой части ограничений прямой задачи, изменяется и оптимальное решение двойственной задачи. узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 19. | Укажите неверное утверждение: а) если прямая задача на минимум не ограничена снизу, то двойственная задача не имеет решения; б) если двойственная задачи на минимум, то ее допустимое решение не больше допустимого решения сопряженной задачи; в) если в сопряженных задачах имеются допустимые решения, при которых целевые функции совпадают, то решения оптимальны. узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 20. | Укажите неверное утверждение: а) если прямая задача на минимум, то ее допустимое решение не меньше допустимого решения сопряженной задачи; б) если прямая задача на максимум, то ее допустимое решение не больше допус- тимого решения сопряженной задачи; в) если прямая задача на максимум не имеет решения, то двойственная задача не ограничена. узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 21. | Укажите неверное утверждение: а) если решение прямой задачи на минимум обращает i-ое ограничение в строгое неравенство, то соответствующая двойственная переменная отлична от нуля; б) если в ограничениях одной из сопряженных задач встречается равенство, то в другой есть переменная, не ограниченная в знаке; в) если в сопряженых задачах имеются допустимые решения, при которых целевые функции совпадают, то решения оптимальны. узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 22. | Укажите неверное утверждение: а) если решение прямой задачи на минимум обращает i-ое ограничение в строгое равенство, соответсвующая двойственная переменная отлична от нуля; б) если прямая задача на минимум, то ее допустимое решение не меньше допустимого решения сопряженной; в) если решение прямой задачи на максимум обращает i-ое ограничение в строгое неравенство, то соответствующая двойственная переменная равна нулю. узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 23. | Укажите неверное утверждение: а) если решение прямой задачи на минимум обращает i-ое ограничение в строгое равенство, то соответсвующая двойственная переменная отлична от нуля; б) если в ограничениях одной из сопряженных задач встречается равенство, то в другой есть переменная, не ограниченная в знаке; в) если прямая задачи на минимум, то ее допустимое решение не меньше допустимого решения сопряженной. узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 24. | Укажите неверное утверждение: а) при всяком изменении правой части ограничений прямой задачи изменяется и оптимальной решение двойственной задачи; б) если прямая задача на минимум не ограничена снизу, то двойственная не имеет решения; в) если в сопряженных задачах имеются допустимые решения, при которых целевые функции совпадают, то решения оптимальны. узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 25. | Укажите неверное утверждение: а) при всяком изменении правой части ограничений прямой задачи изменяется и оптимальной решение двойственной задачи; б) если прямая задача на минимум, то ее допустимое решение не меньше допустимого решения сопряженной задачи; в) если прямая задача на максимум не ограичена сверху, то двойственная не имеет решения. узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 26. | В какой вершине области допустимых решений находится оптимальное решение, если 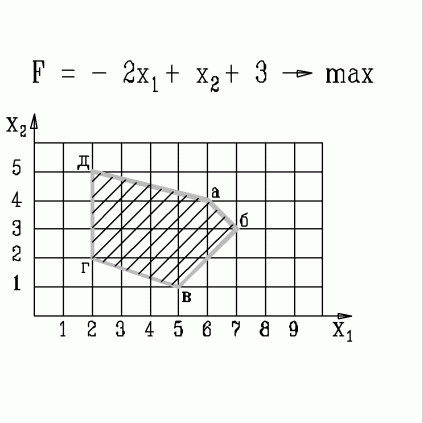 узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 27. | В какой вершине области допустимых решений находится оптимальное решение, если 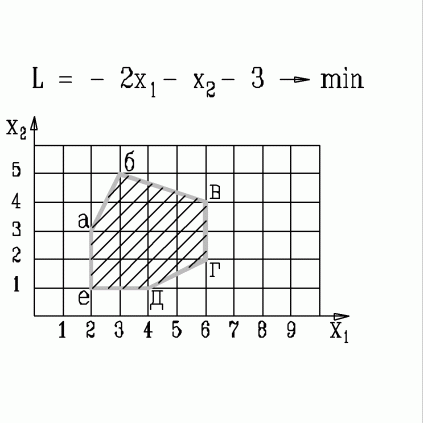 узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 28. | В какой вершине области допустимых решений находится оптимальное решение, если 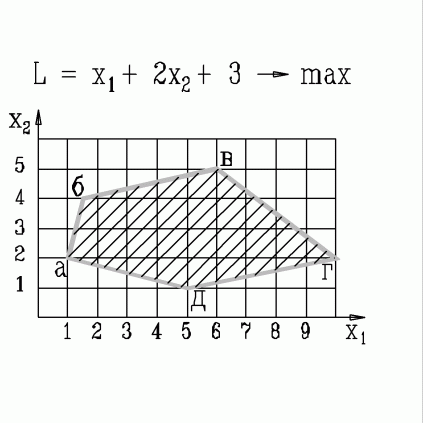 узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 29. | В какой вершине области допустимых решений находится оптимальное решение, если 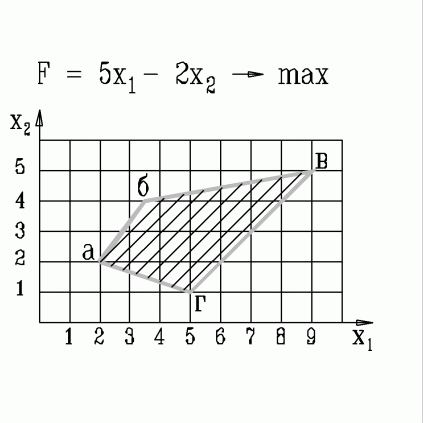 узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 30. | В какой вершине области допустимых решений находится оптимальное решение, если 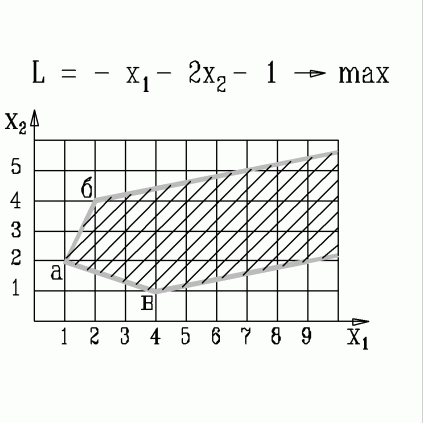 узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 31. | В какой вершине области допустимых решений находится оптимальное решение, если 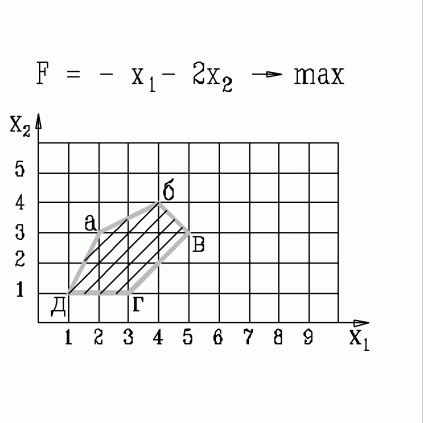 узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 32. | В какой вершине области допустимых решений находится оптимальное решение, если 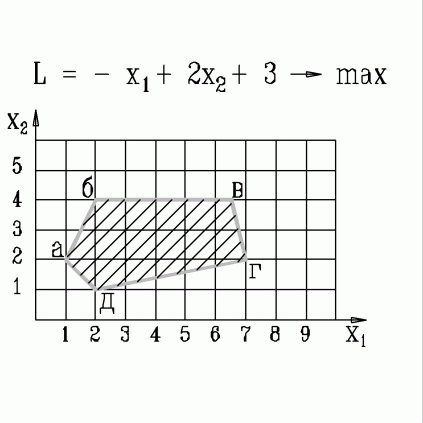 узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 33. | В какой вершине области допустимых решений находится оптимальное решение, если 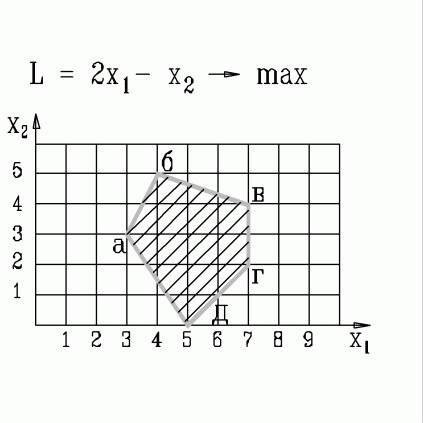 узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 34. | В какой вершине области допустимых решений находится оптимальное решение, если 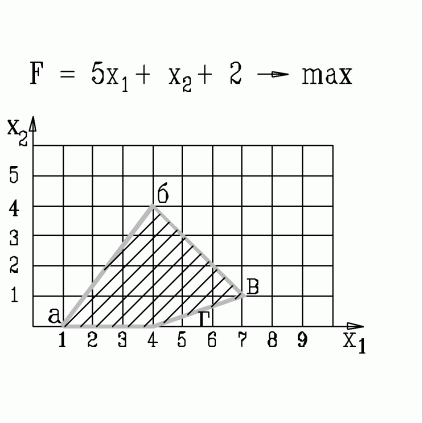 узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 35. | В какой вершине области допустимых решений находится оптимальное решение, если 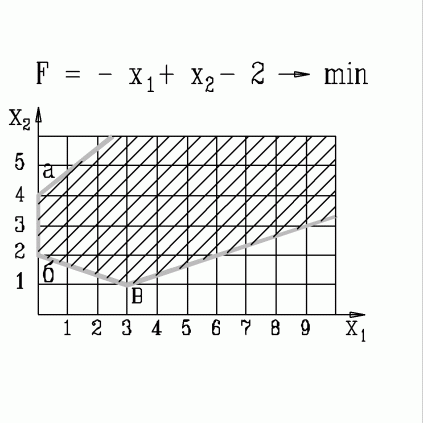 узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 36. | В какой вершине области допустимых решений находится оптимальное решение, если 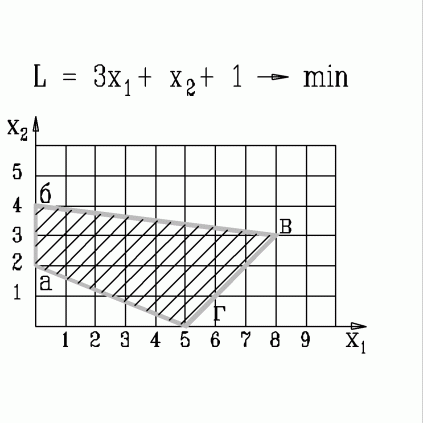 узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 37. | В какой вершине области допустимых решений находится оптимальное решение, если 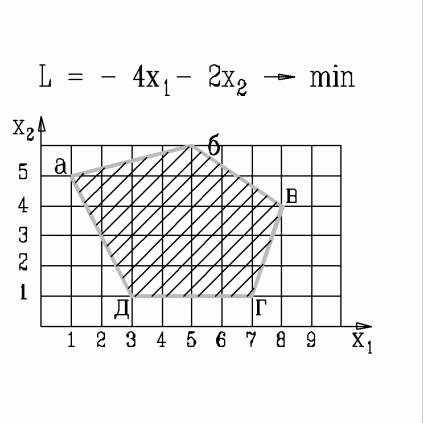 узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 38. | В какой вершине области допустимых решений находится оптимальное решение, если 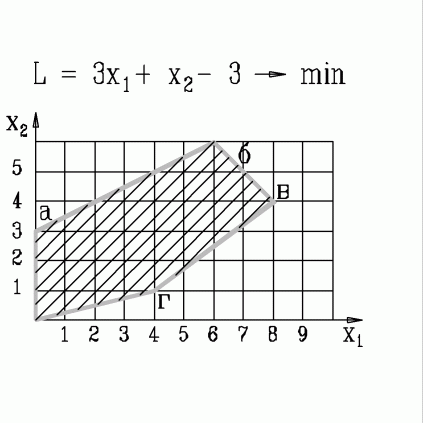 узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 39. | В какой вершине области допустимых решений находится оптимальное решение, если 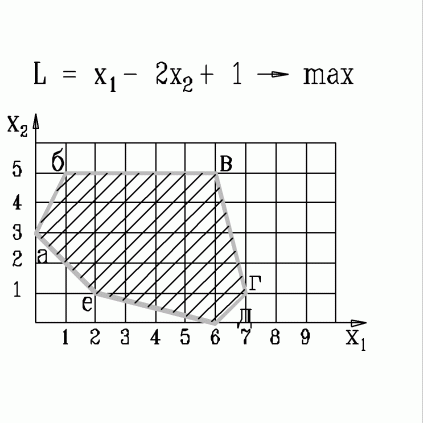 узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 40. | В какой вершине области допустимых решений находится оптимальное решение, если 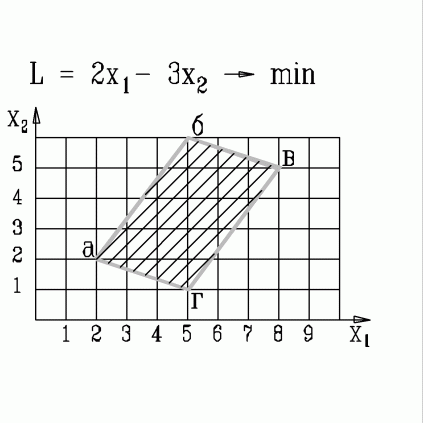 узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 41. | В какой вершине области допустимых решений находится оптимальное решение, если 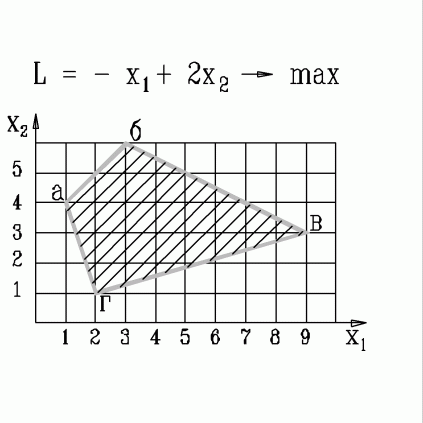 узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 42. | В какой вершине области допустимых решений находится оптимальное решение, если 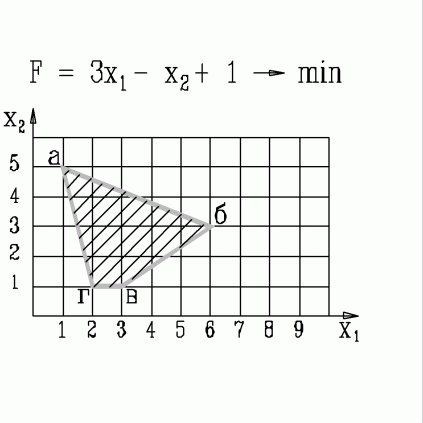 узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 43. | В какой вершине области допустимых решений находится оптимальное решение, если 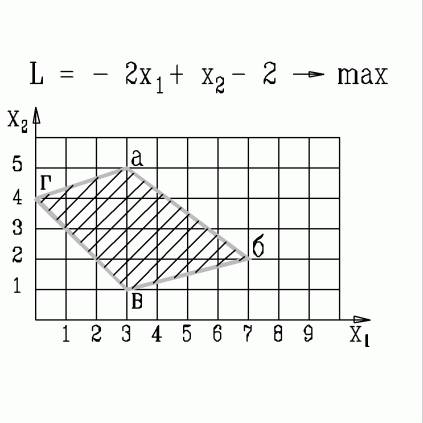 узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 44. | В какой вершине области допустимых решений находится оптимальное решение, если 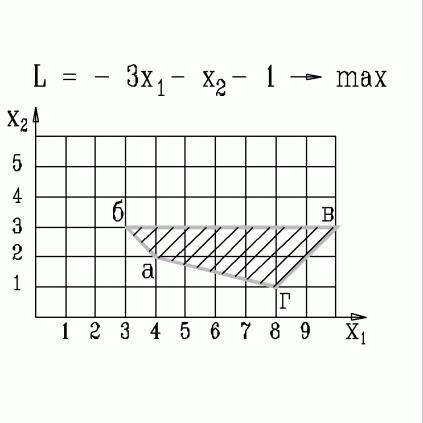 узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 45. | В какой вершине области допустимых решений находится оптимальное решение, если 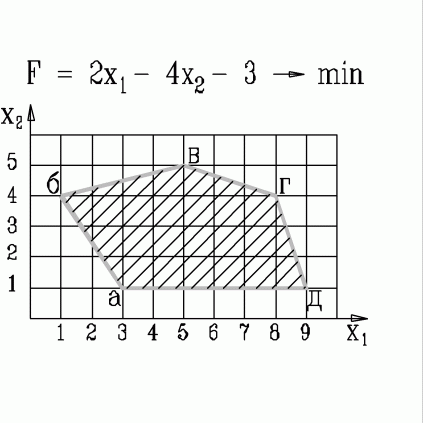 узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 46. | В какой вершине области допустимых решений находится оптимальное решение, если 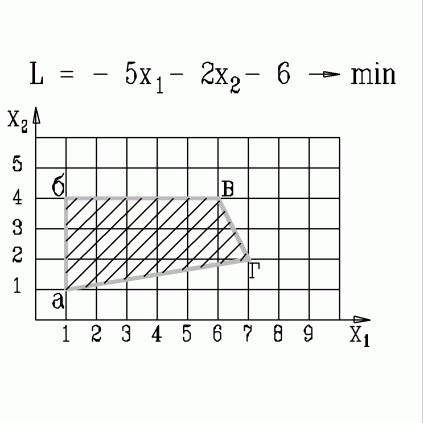 узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 47. | В какой вершине области допустимых решений находится оптимальное решение, если 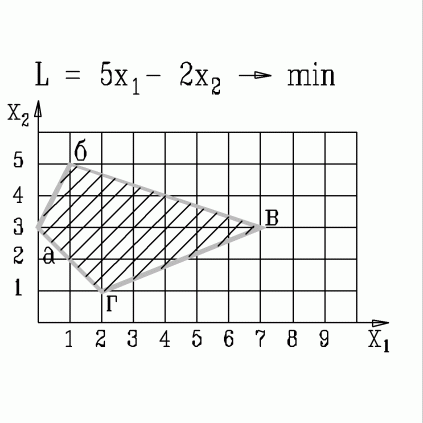 узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 48. | В какой вершине области допустимых решений находится оптимальное решение, если 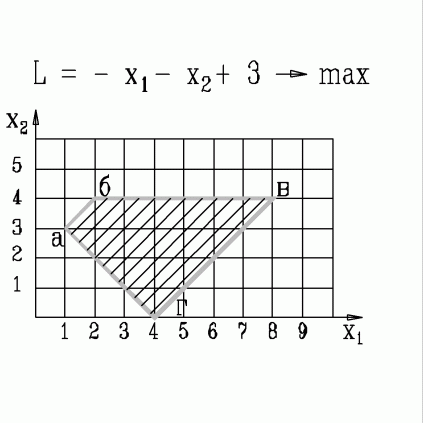 узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 49. | До какого значения можно максимально увеличить целевую функцию при увеличении запаса второго ресурса. 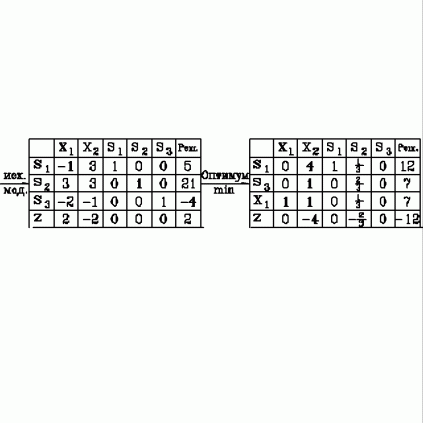 узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 50. | До какого значения можно максимально увеличить целевую функцию при увеличении запаса второго ресурса. 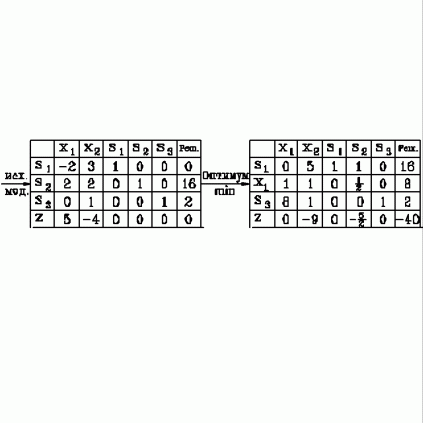 узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
|
Здравствуйте, гость!